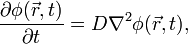The diffusion equation is a partial differential equation which describes density fluctuations in a material undergoing diffusion. It is also used to describe processes exhibiting diffusive-like behaviour, for instance the 'diffusion' of alleles in a population in population genetics.
The equation is usually written as:
where 
is the density of the diffusing material at location 
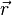and time t and 
is the collective diffusion coefficient for density φ at location 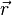; the nabla symbol 
represents the vector differential operator del acting on the space coordinates. If the diffusion coefficient depends on the density then the equation is nonlinear, otherwise it is linear. If 
is constant, then the equation reduces to the following linear equation:
also called the heat equation. More generally, when D is a symmetric positive definite matrix, the equation describes anisotropic diffusion, which is written (for three dimensional diffusion) as:
Derivation
The diffusion equation can be derived in a straightforward way from the continuity equation, which states that a change in density in any part of the system is due to inflow and outflow of material into and out of that part of the system. Effectively, no material is created or destroyed:
,
where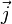 
is the flux of the diffusing material. The diffusion equation can be obtained easily from this when combined with the phenomenological Fick's first law, which assumes that the flux of the diffusing material in any part of the system is proportional to the local density gradient:
.
Historical origin
The particle diffusion equation was originally derived by Adolf Fick in 1855.
Discrete analogs
The diffusion equation is continuous in both time and space. One may discretize space, time, or both space and time, which arise in application. Discretizing time alone just corresponds to taking time slices of the continuous system, and no new phenomena arise. In discretizing space alone, the Green's function becomes the discrete Gaussian kernel, rather than the continuous Gaussian kernel. In discretizing both time and space, one obtains the random walk.
